Dreieck berechnen, Winkel berechnen
Fläche, Winkel und Hypothenuse beim rechtwinkligen Dreieck
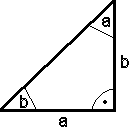
Auch beim Bauen kommt es immer wieder mal vor, dass man Berechnungen zu einem rechtwinkligen Dreieck anstellen muss. Beispielsweise hilft die Berechnung der Hypothenuse bei der Errichtung eines Schnurgerüstes. Auch wenn man Wände (Mauern oder Trockenbau) stellen will, sollte dies im rechten Winkel geschehen.
Tipp - wenn man keinen Taschenrechner oder keinen Zugang zu unserer Berechnungshilfe hat:
Eine einfache Formel für den rechten Winkel:
a = 0,30 b = 0,40 und c = 0,50 cm. Diese 3 4 5 Regel garantiert immer einen rechten Winkel. Z.B.: eine Seite 3 Meter, die andere 4 Meter und die Diagonale = 5 Meter.
Hier ein Formular zum Berechnen der Hypothenuse:
Ergebnisse
| Hypotenuse (c): | |
| Fläche (m²): |
Online-formular zum Berechnen der Winkel
Mit diesem Formular kann man einfach Winkel und Seiten eines Dreiecks berechnen:
Ergebnisse
| Winkel α (Grad): | |
| Winkel β (Grad): | |
| Winkel γ (Grad): |
Die Berechnung funktioniert nur wenn Java Skript aktiviert ist.
Grundlage bei der Berechnung der Hypotenuse ist der Satz des Pythagoras. Dieser besagt, dass die Summe der Flächen der Kathetenquadrate gleich der Fläche des Hypothenusesnquadrates ist.
Zudem hat man mit dieser Formel die Möglichkeit sicher zu stellen, dass Bauteile exakt im rechten Winkel zueienander stehen.
